Distribuzione Binomiale nel Gioco del Lotto: Un’Analisi delle Probabilità
Nel gioco del Lotto, ogni estrazione è un evento indipendente e casuale, ma gli appassionati spesso cercano di utilizzare modelli statistici per cercare di fare previsioni o analizzare le estrazioni. Uno degli approcci più comuni per trattare eventi con esito dicotomico (successo o insuccesso) in un numero fisso di prove è la distribuzione binomiale. Sebbene non si possa prevedere con certezza l’estrazione di numeri specifici, l’uso della distribuzione binomiale può fornire un’analisi interessante per comprendere le probabilità di ottenere un certo numero di estrazioni corrette su più tentativi.
Cos’è la distribuzione binomiale?
La distribuzione binomiale è una distribuzione di probabilità discreta che descrive il numero di successi in un numero fisso di prove indipendenti, in cui ogni prova ha due esiti possibili: successo o fallimento. Un esempio di questo tipo di esperimento potrebbe essere il lancio di una moneta (testa o croce), ma nel contesto del Lotto, un “successo” può essere definito come l’estrazione di un numero specifico in una determinata estrazione.
La funzione di probabilità della distribuzione binomiale è:
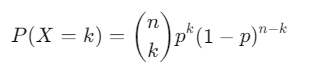
Dove:
- n è il numero di prove (nel caso del Lotto, il numero di estrazioni in cui si vuole determinare la probabilità di successo).
- k è il numero di successi (quanti numeri indovinati si vogliono ottenere).
- pp è la probabilità di successo in una singola prova (la probabilità che un numero specifico venga estratto).
- 1−p è la probabilità di fallimento (la probabilità che un numero non venga estratto).
- (n k) è il coefficiente binomiale, che rappresenta il numero di modi in cui si possono scegliere k successi da n prove.
Applicazione della distribuzione binomiale nel Lotto
Nel contesto del gioco del Lotto, la distribuzione binomiale può essere utilizzata per calcolare la probabilità di ottenere un numero definito di numeri estratti correttamente in una serie di estrazioni. Immagina, ad esempio, che tu stia cercando di indovinare 2 numeri su 5 estratti su una ruota, e che tu stia partecipando a 10 estrazioni.
- La probabilità di successo, p, è pari a 5 estrazioni corrette su 90 numeri, quindi la probabilità di successo per ogni singolo numero è p = 5/90 ≈ 0,0556
- n è il numero di estrazioni a cui partecipi, ad esempio 10 estrazioni
- k è il numero di successi che stai cercando (ad esempio, indovinare 2 numeri corretti in una data estrazione)
Usando la formula della distribuzione binomiale, puoi calcolare la probabilità di indovinare esattamente 2 numeri in una sequenza di 10 estrazioni.
Esempio pratico
Supponiamo che tu voglia sapere qual è la probabilità di indovinare esattamente 2 numeri in 5 numeri estratti su 10 estrazioni (ad esempio, se giochi 10 volte su una ruota del Lotto).
Impostiamo i valori:
- n = 10 (numero di estrazioni).
- k = 2 (successi desiderati, ovvero 2 numeri corretti).
- p = 5/90 ≈ 0,0556 (probabilità di indovinare un singolo numero su 90).
La probabilità di indovinare esattamente 2 numeri su 5 in 10 estrazioni sarà:
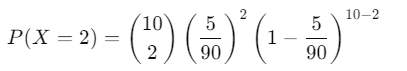
Questa formula ti darà la probabilità di ottenere esattamente 2 numeri corretti su 10 estrazioni.
Limiti nell’applicazione della distribuzione binomiale nel Lotto
- Indipendenza delle estrazioni: Ogni estrazione è un evento indipendente, il che significa che la probabilità di indovinare un numero non cambia da una estrazione all’altra. Anche se un numero non è stato estratto per molte estrazioni, la sua probabilità di essere estratto rimane costante in ogni estrazione.
- Combinazioni più complesse: Sebbene la distribuzione binomiale possa essere utile per calcolare la probabilità di successo con un numero definito di estrazioni e successi, non è facilmente applicabile a combinazioni più complesse, come quelle che coinvolgono numeri ritardatari o la previsione di una cinquina completa.
- Probabilità di successo costante: La distribuzione binomiale presuppone che la probabilità di successo rimanga costante in ogni prova. Tuttavia, nel Lotto, la probabilità di estrazione di un numero rimane fissa (5 numeri su 90), ma non tiene conto di fattori complessi come i ritardi o i pattern che alcuni giocatori tendono a osservare.
Conclusioni
La distribuzione binomiale offre un utile strumento per analizzare le probabilità di ottenere un determinato numero di numeri corretti in un set di estrazioni del Lotto. Utilizzando la probabilità di successo di un singolo numero estratto e applicando il modello binomiale, è possibile calcolare la probabilità di indovinare un certo numero di numeri in un periodo definito di estrazioni. Tuttavia, è importante ricordare che, come per tutte le distribuzioni di probabilità, la distribuzione binomiale non può garantire alcun tipo di vincita, poiché il gioco del Lotto è un gioco puramente casuale. Nonostante ciò, la distribuzione binomiale fornisce una base statistica per analizzare il gioco, ma non deve essere vista come una “strategia infallibile”.






