La Distribuzione Poisson nel Gioco del Lotto: Un’Analisi Statistica

Nel gioco del Lotto, ogni estrazione è un evento casuale, ma molti appassionati cercano di applicare modelli matematici per analizzare le estrazioni passate e prevedere future. Una delle distribuzioni più utilizzate per modellare eventi casuali in un determinato intervallo è la distribuzione Poisson. Sebbene il Lotto sia un gioco basato esclusivamente sulla casualità, la distribuzione Poisson può essere utile per analizzare la frequenza con cui i numeri vengono estratti nel tempo e per comprendere la probabilità che un numero venga estratto un determinato numero di volte in un certo periodo.
Cos’è la distribuzione Poisson?
La distribuzione Poisson è un modello statistico che descrive la probabilità che si verifichino un certo numero di eventi in un intervallo di tempo o spazio, a condizione che questi eventi siano rari e indipendenti. È particolarmente utile per descrivere situazioni in cui gli eventi sono distribuiti in modo casuale e con una media costante di occorrenze.
La formula della distribuzione Poisson è:
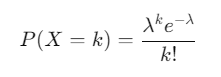
Dove:
- λ lambda è la media di eventi attesi in un determinato intervallo (ad esempio, la media delle estrazioni di un numero).
- k è il numero di eventi (ad esempio, il numero di volte che un determinato numero viene estratto).
- e è la base dei logaritmi naturali (circa 2.71828).
Probabilità di estrazione di un numero al Lotto
Nel gioco del Lotto, per ogni ruota, vengono estratti 5 numeri su un totale di 90. La probabilità che un numero specifico venga estratto in una singola estrazione è di 1 su 18 (circa il 5,56%), dato che su 90 numeri complessivi, 5 numeri vengono estratti per ogni ruota.
Tuttavia, la probabilità di estrazione di un numero in più estrazioni successive dipende dalla sua frequenza storica e dalla natura casuale delle estrazioni. In questo contesto, la distribuzione Poisson può essere applicata per determinare la probabilità che un numero venga estratto un certo numero di volte in un periodo definito, assumendo che ogni estrazione sia indipendente e che la probabilità di estrazione di ciascun numero resti costante.
Applicare la distribuzione Poisson al Lotto
Per applicare la distribuzione Poisson al Lotto, bisogna raccogliere i dati storici delle estrazioni e calcolare il numero medio di volte che un numero viene estratto in un periodo definito, ad esempio, durante un mese o un anno. Supponiamo che, in media, un numero venga estratto 5 volte su 100 estrazioni. Questo valore diventa il nostro parametro λ lambda. Successivamente, possiamo utilizzare la formula di Poisson per calcolare la probabilità che un numero venga estratto 6 volte, nessuna volta, o un’altra quantità definita di volte in un periodo di 100 estrazioni.
Un esempio pratico
Immagina che tu voglia sapere qual è la probabilità che un numero venga estratto 7 volte in 100 estrazioni, se la media storica di estrazione è di 5 volte.
- λ=5 (media storica di estrazioni di quel numero).
- k=7 (numero di estrazioni che vogliamo calcolare).
- Utilizzando la formula di Poisson:
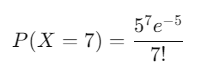
Il risultato di questo calcolo darà la probabilità di vedere quel numero estratto 7 volte in 100 estrazioni.
Limiti nell’uso della distribuzione Poisson nel Lotto
Nonostante la distribuzione Poisson offra un interessante approccio statistico per analizzare la frequenza con cui i numeri vengono estratti, ci sono diversi limiti nell’applicazione di questo modello al gioco del Lotto:
- Indipendenza delle estrazioni: Ogni estrazione è un evento indipendente. Pertanto, non esiste una “memoria” tra le estrazioni e un numero ritardatario non ha più probabilità di essere estratto rispetto a qualsiasi altro numero.
- Campioni limitati: Poiché il Lotto è un gioco con un numero relativamente basso di estrazioni (5 numeri su 90), l’applicazione della distribuzione Poisson su periodi brevi potrebbe non essere sempre rappresentativa del comportamento futuro delle estrazioni.
- Combinazioni complesse: La distribuzione Poisson è utile per analizzare la frequenza di estrazione di singoli numeri, ma non è facilmente applicabile alle combinazioni di numeri o alle cinquine complete di numeri estratti.
Conclusione
La distribuzione Poisson offre un interessante strumento teorico per analizzare le probabilità delle estrazioni nel gioco del Lotto, ma non cambia la natura puramente casuale delle estrazioni. Sebbene questa distribuzione possa essere utilizzata per analizzare la frequenza storica dei numeri estratti e prevedere la probabilità di estrazione futura di un determinato numero, non può alterare le probabilità intrinseche del gioco. Alla fine, il Lotto rimane un gioco di casualità pura, e la distribuzione Poisson serve più che altro come un esercizio matematico per esplorare le probabilità statistiche piuttosto che come una strategia concreta per vincere.






