Glossario – Calcolo combinatorio

Il calcolo combinatorio è un procedimento matematico che restituisce il numero di combinazioni possibili, data una determinata serie di numeri.
Qui sotto la formula:
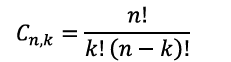
La formula spiegata:
Cn,k = il numero di combinazioni possibili (senza ripetizioni) con n oggetti di cui k utilizzati
n = il numero di oggetti che si possono utilizzare per calcolare le combinazioni possibili
k = il massimo di oggetti utilizzabili per creare una combinazione
n! = il fattoriale di n
k! = il fattoriale di k
! = il fattoriale si calcola moltiplicando tutti i numeri interi partendo dal numero definito (togliendo una unità ad ogni numero successivo) fino ad 1.
Esempio di fattoriale – il di 5 si calcola così: 5*4*3*2*1 = 120
Ipotizzando di voler scoprire quante cinquine si possono ottenere con 10 numeri e, seguendo la formula qui sopra dobbiamo prima definire le variabili n e k:
n=10 – i numeri totali che utilizzeremo per fare il calcolo
k=5 – i numeri che utilizzeremo per ogni singola combinazione
Calcoliamo così:
(n!) ossia 10! = 10*9*8*7*6*5*4*3*2*1 = 3.628.800
(k!(n-k)! ossia 5!(10-5)! = (5*4*3*2*1)5! = 120*120 = 14.400
dividiamo 3.628.800/14400 = 252
Con 10 numeri si possono quindi formare 252 cinquine univoche, ossia senza ripetizioni.








