Glossario – La legge dei grandi numeri

La legge dei grandi numeri o teorema di Bernoulli (Jakob Bernoulli fu il primo a formulare questa teoria) descrive il comportamento della media di una sequenza di prove di una variabile casuale indipendenti e caratterizzate dalla stessa distribuzione di probabilità.

Con un numero abbastanza grande di prove, ogni evento si manifesta con una frequenza che si avvicina alla probabilità teorica e, più è alto il numero delle prove, più la frequenza di avvicina alla probabilità teorica.

Questa è la variabile di Bernoulli:

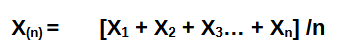
Con questa formula si afferma che, all’aumentare della dimensione del campione di analisi, la media degli eventi si avvicina al valore teorico.

Per esempio, lanciando una moneta, la probabilità che esca testa è del 50%; se continuassimo a lanciare la moneta per 100 o 1000, vedremo che il numero degli eventi “testa” si avvicinerà sempre di più al 50%.

Se prendiamo il Gioco del Lotto invece, sappiamo che la probabilità di estrazione di 1 numero ad ogni estrazione è di 1/18; da qui possiamo teoricamente dedurre che in 18 estrazioni dovrebbero uscire tutti i 90 numeri, infatti moltiplicando 18 * 5 = 90.

Naturalmente non è così ma, se prendessimo in esame il tabellone delle frequenze, salterebbe immediatamente agli occhi che la frequenza di estrazione dei 90 numeri è molto simile tra loro.