Glossario – Probabilità

Introduzione alla Probabilità Matematica: Capire l’Incertezza
La probabilità matematica è un ramo della matematica che studia la possibilità che si verifichi un evento. Questa scienza è fondamentale per prevedere fenomeni casuali, come i risultati di giochi, eventi naturali, o anche il rischio in finanza e assicurazioni. Grazie alla probabilità, possiamo quantificare l’incertezza e fare previsioni su un’ampia gamma di eventi.
La Definizione di Probabilità
La probabilità di un evento è un numero che va da 0 a 1 e indica la possibilità che l’evento accada. Un evento impossibile ha probabilità 0, mentre un evento certo ha probabilità 1. Ad esempio, lanciare una moneta e ottenere “testa” ha una probabilità di 0,5 (50%), poiché ci sono due possibili risultati uguali.
Calcolo della Probabilità
Le formule della probabilità sono basate su diversi approcci. Uno dei più semplici è il calcolo classico, che riguarda eventi con risultati equiprobabili, cioè con probabilità uguali, come nel lancio di dadi o di monete. Si calcola come:
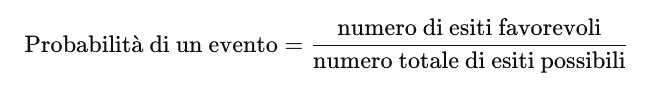
Ad esempio, la probabilità di ottenere un 6 lanciando un dado è di 1 su 6.
Probabilità e Eventi Dipendenti
Non tutti gli eventi sono indipendenti. Alcuni fenomeni hanno una probabilità condizionata, cioè la probabilità che un evento accada può dipendere da un altro evento già accaduto. Questo concetto è essenziale nelle analisi di rischio e nelle previsioni basate su dati reali.
Per definizione esistono tre “tipi” di probabilità
La probabilità può essere analizzata attraverso diverse prospettive e, le tre principali sono la probabilità classica, la probabilità frequentista e la probabilità soggettiva. Ecco una breve spiegazione di ciascuna:
- Probabilità Classica: Questo approccio si basa sull’idea che tutti gli eventi siano equiprobabili. La probabilità di un evento è calcolata come il numero di esiti favorevoli diviso il numero totale di esiti possibili. Ad esempio, nel lancio di un dado, la probabilità di ottenere un 3 è 1 / 6 perché ci sono sei esiti possibili e solo uno di essi è il 3.
- Probabilità Frequentista: La probabilità in questo contesto è definita come il limite della frequenza relativa di un evento man mano che il numero di prove aumenta. Se un evento si verifica ( n ) volte in ( N ) prove, la probabilità dell’evento è data da (P(E)=N/n). Questo approccio si basa sull’osservazione di esperimenti ripetuti e sulla raccolta di dati empirici.
- Probabilità Soggettiva: A differenza delle altre due, la probabilità soggettiva si basa sulle opinioni e sulle credenze personali di un individuo riguardo alla verità di un evento. Non si basa necessariamente su dati storici o su esperimenti ripetuti. Ad esempio, una persona potrebbe attribuire una probabilità del 70% a una certa squadra di calcio per vincere una partita basandosi sulle proprie valutazioni, intuizioni e informazioni disponibili.
Questi approcci possono coesistere e vengono utilizzati in contesti diversi, a seconda delle necessità analitiche e delle informazioni disponibili.
Conclusione
La probabilità matematica è uno strumento che ci permette di gestire l’incertezza con precisione. Ci aiuta a prendere decisioni più informate, prevedendo l’incidenza di eventi futuri e aumentando la nostra comprensione del mondo in termini di probabilità.








